Game-based Introduction to Algorithms

In this workshop we will play a number guessing game to introduce participants to algorithmic logic. This can be used as an introduction to a longer series on programming and digital thinking.

Trace the following flowchart on the floor using chalk or masking tape. The boxes should be big enough for one participant to stand inside.

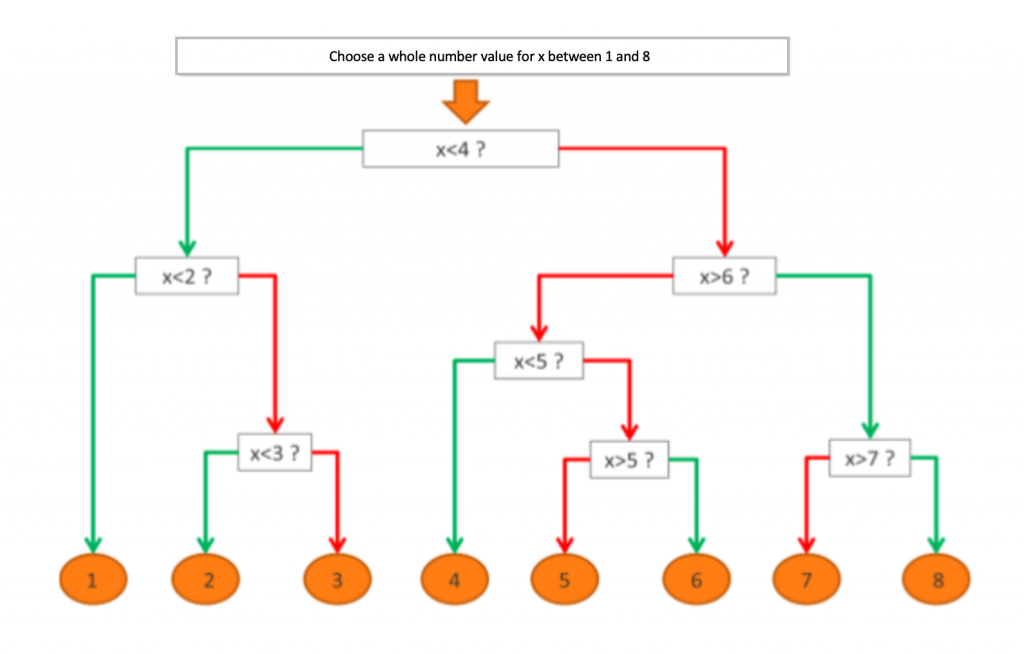
It is important that the arrows correspond to the colours shown here according to whether the received answer is positive or negative. To avoid ambiguity, you can also write ‘yes’ and ‘no’ on the appropriate branches.

As an introduction, we will demonstrate the advantages of algorithms and pique the participants’ curiosity with an approach invoking mystery and challenge. Adapt the below explanation according to the age of your audience – the way it is presented now is designed for those around 12 years old.

Tell the participants that you have learned to do a magic trick : you can guess the number someone is thinking between 1 and 8 following a maximum of four questions! Prove it: ask a group member to secretly choose a number and ask them a question by following the prepared diagram directly. You could then repeat the process with another participant to show that you can get the number in three (or four) attempts each time.
Reveal that it is not really magic but that you have followed an algorithm. Explain that an algorithm is a series of simple and precise steps (instructions). These must be followed to arrive at a goal or the solution to a problem.

An algorithm can take many forms depending on its purpose: a recipe is an algorithm for making a dish, a route is an algorithm for arriving at a destination, a mathematical formula is an algorithm for making calculations, etc. With adolescents, you can ask them to guess/find other examples of algorithms. In this case, you should be capable of confirming or explaining why a given example is right or wrong.

Explain that you are going to teach them to do the ‘magic trick’ themselves. Show the flowchart you have prepared on the floor and show them how to read it : go to the beginning, choose a number, ask the question, ‘respond’ to the question by following the ‘yes/no’ line, and so on. The final box gives the result. Explain that a number is no bigger or smaller than itself, by using an example like ‘if you take 9 as the given number, and I ask you if your number is smaller than 9, the answer is no’.

Ask the group to divide into pairs and use the flowchart together: one person chooses a number and goes to the flowchart while the other asks them question and tells them how to progress through the flowchart. Leave a few minutes for the group to complete the exercise, ideally twice for each duo so that each person can play both roles. Stay engaged to correct potential mistakes.

Link your previous explanation of algorithms and the real algorithm that was just used: it was comprised of steps (questions), execution of simple and clear instructions (there are only ever two possible responses – we always know how to respond), and we arrived at the end, we get an unambiguous answer.

Emphasise the fact the to using a ruleset/flowchart like this allows us to easily follow the steps, but that algorithms take on many forms: through video (cooking recipe), in text (maths formula), on a map (directions/route). Connect this to algorithms used in IT. We processed information (the number to be guessed) in an automatic fashion (by following the flowchart, we did not ‘think’ at each step about we were going to do). This is what computers do constantly: process information automatically by following algorithms!

Online variant (for a group familiar with Scratch) You can leave 30 minutes for the group to create the algorithm on Scratch.

Variant for further exploration of algorithms :With a group of 14 years old and older, you can extend the session to cover algorithmic logic in greater depth and to show the limits of computers.
Underline that there is no need for reflection while we follow a schematic. However, we do need to reflect in order to create a schematic such as how can we guess a number most efficiently ?
You can either explain the reasoning below or recreate it practically by using guided questions or a debate, or even (for over-16s) leave them search for the answer themselves : to guess quickly, we first have to quickly eliminate a maximum number of possibilities.
Mark the numbers 1-8 on an axis and indicate the subgroups you will highlight to illustrate your point. From 1-8 there are 8 possibilities. If your first questions is at one of the extremities of the axis, for example ‘if the number larger than 7?’, there is only one possible response (8). If the answer is yes, congratulations, you’ve found it one step ! But this requires luck.
If the response is no, up to 7 steps remain ! We have therefore not reduced the number of possibilities sufficiently. But if we ask a question concerning the centre of the axis (‘is the number smaller than 4?), only four possibilities will remain regardless of the answer. We have in this case halved the number of possible answers.

In other words, we are already half-way towards a solution! Look now at the algorithm’s flowchart : at each step, we go to the halfway point of the remaining possibilities. This is the quickest way to the solution. Regardless of the chosen number, there will only ever be three, maximum four questions.

This is how we took a problem (guess a number), reflected on how to solve it in the best way (here, the quickest way), and adapted the solution to the form of an algorithm. Anyone can use this algorithm without needed to redo the conceptualisation stage. Computers work the say way : they do not think! Someone does the thinking in advance (the programmer) in order to create the algorithms (programs) and the computers just follow these.
Sometimes, there are so many algorithms put together doing different things that it gives the impression that the computer is thinking, but this is not the case. For example when ask questions to Siri, Google or Alexa with a smartphone, there are several algorithms used to capture and identify the words, then others for trying to guess what we are asking, yet more for finding the answers and finally others to imitate speech and say the answer.

With a group of over 14s, you can conclude by giving some examples of simple expanded algorithms and their advantages in IT:

• The site Akinator (which guesses the identity of the person we are thinking of) relies on the same principle discussed in the workshop but with a much more developed tree of possibilities. Same for the game Guess Who?
• Calculation algorithm or the Euclid algorithm (watch the videos linked below to inform the discussion, but take care not to break the flow if you choose to show it): when we want to find the greatest common denominator for two numbers, we can follow this method. But this is long and quite laborious when we need to process a large number. The Euclid algorithm offers a simpler way to find the greatest common denominator between two numbers.
• Search algorithms: this is what search programs use for example the one we encounter when we search for a file in a hard drive.
• PageRank algorithm: this was founded by the same people who founded Google. It means that webpages can be classed according to their popularity. If you find a way to improve how it works, your financial future is assured!
• Facial recognition algorithms: used by Facebook amongst others, these mean that computers can recognise people from their photos.
• Travel website algorithms: these select different possibilities depending on hours, dates, places available, the user’s budget, etc.