Introduction to Sorting Algorithms

In this workshop, participants will first learn about different sorting algorithms. They will then make a cooperative sorting algorithm following a sorting network traced along the floor.

Draw this pattern on the floor (using chalk or masking tape) :

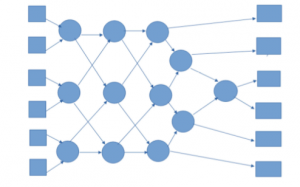
Variants :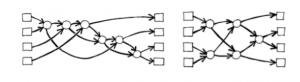

If you would like to use numbers in the second section, print or write a number for each participant in advance. To avoid ambiguity, each number should be used only once.

Give participants the following context: In the world of IT, we would prefer not have to tell computers everything they need to do. We would prefer for example to give the computer a cake recipe once so that it could repeat the instruction many times. We call these ‘recipes’ algorithms. Amongst the most well-known are sorting algorithms.

The problems these solve are simple: for example you might have a series of objects you would like to arrange by size. Tell participants to arrange themselves in a line. One person should be chosen to be the ‘sorter’. Choose together the sorting criteria (age, height, shirt colour – the easiest being the height) and the order (ascending or descending), then ask the sorter to put participants in order (by verbally instructing each person in turn to move to their correct position). Ask the sorter to explain how they managed to complete the task (no need to be precise, just to emphasise that they executed a sorting method). Ask the group is someone has another idea of how it could be done.
If yes, this person now becomes the sorter. The group shuffles themselves again on the sorting reoccurs.
If no one has an idea, you can do it yourself, for example by sorting from one end to the others (bubble sort) : comparing the first two people, sorting them if necessary, then comparing the 2nd to the 3rd person, sorting them if necessary, and so on until the end of the line, then starting again until the whole line is sorted.

Ask the group to compare the two sorting methods: does one seem better than the other ? Why ? Underline the principle idea : the most important factor is the time is takes; the faster the method, the better.
But what determines the time it takes ? The number of comparisons (calculations) done, the point of departure (the more disorder, the more time will be needed) and the number fo elements to sort (the more elements, the more time required).

Explain that there are many ways to sort elements. Not all methods have the same efficiency – some will require more calculations than others. Give an example of sorting by selection: we take the smallest object, we put it first and then we start again. When we start to sort a large number of elements, this approach is no longer efficient. Ask participants what in their opinion is a ‘large number of elements’. If we are talking billions for example, we would need to find more efficient methods. One of these is cooperation.

The principle here is simple: if the whole class is baking a cake, the job will be done quicker that if one person needs to bake for everyone. We will play a simple game to illustrate this idea.

1. Divide participants into groups of 6.
2. Each group member chooses a hard and places it randomly on one of the 6 starting boxes on the network outlined on the floor.
3. Next each person follows their line, arriving at a circle and waiting until another player arrives
4. When there are two people on a circle, they compare their numbers. Those with the smaller number takes the left-hand path and the other takes the right.
5. Continue until the other side is reached.

Tell participants that they have now been categorised. Ask how many calculations (comparisons) were executed simultaneously each time. Answer: 3. Mention that if one participants had to do all the comparisons, it would have taken them much more time (and they would felt quite alone…).

You should conclude on the advantages of sorting networks. Participants will have already realised that sorting algorithms are quicker than regular algorithms but that they also use more resources (for example 3 ‘computers’). Obviously, these are used to sort large amounts of data.

Try to find other example where the idea of simultaneous/parallel action is more efficient. (Examples: sorting books, serving meals. Examples from science to emphasise importance : Facebook and the size of its database – it has several billion users with scores of data (names, ages, places of residence, occupation) which has to be sorted.
Parallel sorting algorithms are of course used for this. Depending on the age of the participants you can continue : today in fact, scientists use this technique extensively since the amount of data processed now has become almost unimaginably enormous.

With the digital revolution, the amount of data available to the public has exploded. Scientists and engineers in particular need to process more data than ever. ‘Big data’ is here to solve this problem. It consists in the reduction and synthesising of the quantity of information.

What is interesting is that the concept that hides behind this is parallel programming. We sort the data between a huge number of computers, each addressing their own part of the data. They are then linked up.